Deep learning has been successfully applied to a variety of tasks.
On real-time scenarios such as inference on autonomous vehicles, the inference speed of the model is critical.
Network quantization is an effective approach to accelerating deep learning models.
In quantized models, both data and model parameters are represented with low precision data types such as int8 and float16.
The lowered data bandwidth reduces the inference time and memory/storage requirements, as well as the power consumption.
Meanwhile, under proper quantization schemes, we can minimize the accuracy drops of the quantized models.
Therefore, quantized models are of particular interests of researchers and developers as it makes large models suitable to deploy on diverse devices, such as GPU, CPU and mobile devices.
Previously, quantized operators are usually optimized with handcrafted microkernels for different workloads, or rely on blackbox proprietary solutions such as cuDNN and TensorRT. Writing a high-performance microkernel in assembly can be very challenging and usually requires heavy engineering effort. Besides, it is difficult to adapt these ad-hoc microkernels to emerging workloads and new devices.
TVM solves this challenge with a full stack compiler and a machine-learning-based optimizer to automatically generate computing kernels. TVM can generate efficient kernels via automatic search in a human-designed search space. In standard workloads such as VGG and ResNet, TVM achieves competitive performance compared with other state-of-the-art frameworks. In emerging models such as ResNeXt and Deformable ConvNets, the automatic optimization makes it easy for TVM to adapt to these new workloads and achieve a significant performance boost.
In this post, we show how to use TVM to automatically optimize of quantized deep learning models on CUDA.
Expressing Quantized CUDA Kernels in TVM
Leveraging Tensor Intrinsics via Tensorization
Many platforms provide architecture-specific instructions for special computation patterns, for example, the SIMD instructions on x86, and the dp4a and hfma instructions on CUDA.
These intrinsic instructions are highly optimized for specific devices.
By leveraging hardware intrinsics, we can achieve a significant performance boost for quantized operators.
Currently, dp4a has been extensively used in TVM int8 operators on CUDA.
dp4a is a CUDA intrinsic on Compute Capability 6.1 devices.
It is a mixed-precision instruction that provides the efficient computation of the dot product between two 4-element 8-bit integer vectors and accumulates the result in 32-bit format.
Using dp4a, we can implement a dot product between 8-bit integer vectors with number of elements evenly divisible by four.
With an efficient dot product operator, we can implement high-level operators such as 2d convolution and dense layers as these operators are commonly backed by dot products.
To illustrate, in 2d convolution we accumulate along the channel, the width, and the height axis of the kernel.
This is a typical use case of dp4a.
TVM uses tensorization to support calling external intrinsics.
We do not need to modify the original computation declaration; we use the schedule primitive tensorize to replace the accumulation with dp4a tensor intrinsic.
More details of tensorization can be found in the tutorial.
Data Layout Rearrangement
One of the challenges in tensorization is that we may need to design special computation logic to adapt to the requirement of tensor intrinsics.
Although it is natural to accumulate along the inner axis of the tensor in the dense operator, conv2d can be more challenging.
In conv2d we expect to take a slice in the channel dimension as the input of dp4a because the number of channels is typically multiple of 4 (otherwise we fall back to original conv2d in NCHW layout).
Meanwhile, to achieve memory locality, we would like to reduce along the innermost axis first.
Taking these factors into account, we use a custom data layout to address this challenge.
In CUDA int8 2d convolution, we empirically choose NCHW4c as data layout and OIHW4o4i as weight layout.
The templates can also be easily generalized to NCHW[x]c and OIHW[x]o[x]i, where x is an arbitrary positive integer divisible by four.
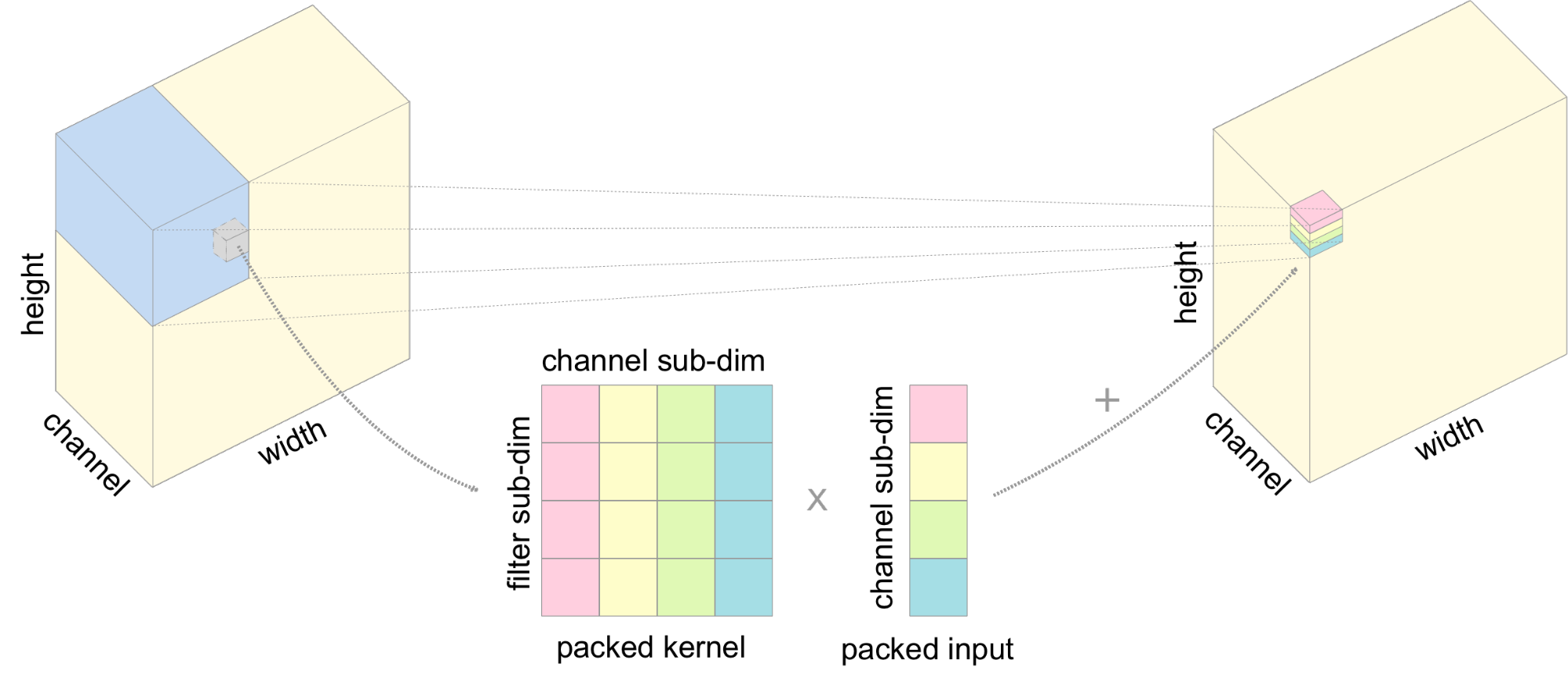
In the data layout we choose, slices of channels are in the packed innermost dimension.
Likewise, we pack slices in both the input and output channel dimensions of the weight so that the output has a consistent data layout with the input, which prevents redundant layout transformations between layers.
We show the computation of one element of the output of the 2d convolution in Figure 2.
The element in each position of the super dimension (the outer dimension of the blocked layout which contains packed elements) NCHW and OIHW is the packed input and kernel, respectively.
Each column of the packed kernel comes from a different filter.
We calculate the dot product between the packed input and each row in the packed kernel using dp4a, and accumulate the result to the output tensor.
After we have specified the layout of convolution layers, other operators such as add and activations can automatically adapt to the chosen layout during the AlterOpLayout pass in Relay.
The layout transformation of the weight can be precomputed offline. Therefore, we can run the whole model in the same layout without extra overhead.
Designing Search Space for Automatic Optimization
The key to achieving good performance in our quantized operators is to integrate with machine-learning-based automatic optimization. One question is how to design an effective schedule search space. An effective schedule template means that we can obtain good performance in a reasonable number of iterations in automatic tuning. Generally speaking, we strive to define a flexible template to cover different configurations in the search space. On the other hand, we also take advantage of the prior knowledge in performance optimization. For example, as caching data in the shared memory is a common practice in CUDA programming, we utilize shared memory, but we use machine learning to choose the best tile size. We also do some manual tiling such as splitting axes by 4 or 16 to facilitate vectorized memory access.
In quantized 2d convolution, we design a search space that includes a set of tunable options, such as the tile size, the axes to fuse, configurations of loop unrolling and double buffering.
The templates of quantized conv2d and dense on CUDA are registered under template key int8.
During automatic tuning, we can create tuning tasks for these quantized operators by setting the template_key argument.
Details of how to launch automatic optimization can be found in the AutoTVM tutorial.
General Workflow

TVM provides an easy workflow to quantize trained models from other frameworks, automatically optimize operators (with AutoTVM), and deploy to different devices.
First, we use the Relay frontend to import existing models. Here we use an MXNet model with (1, 3, 224, 224) input shape as an example.
sym, arg_params, aux_params = mxnet.model.load_checkpoint(model_path, epoch)
net, params = relay.from_mxnet(sym, shape={'data': (1, 3, 224, 224)}, arg_params=arg_params, aux_params=aux_params)
Next, we use the relay quantization API to convert it to a quantized model.
net = relay.quantize.quantize(net, params=params)
Then, we use AutoTVM to extract tuning tasks for the operators in the model and perform automatic optimization. The AutoTVM tutorial provides an example for this.
Finally, we build the model and run inference in the quantized mode.
with relay.build_config(opt_level=3):
graph, lib, params = relay.build(net, target)
The result of relay.build is a deployable library.
We can either run inference on the GPU directly or deploy on the remote devices via RPC.
Benchmark
To verify the performance of the quantized operators in TVM, we benchmark the performance of several popular network models including VGG-19, ResNet-50 and Inception V3. We also benchmark on DRN-C-26, ResNeXt-50, and DCN-ResNet-101 from Deformable ConvNets to show the performance of emerging models, which contains less conventional operators such as dilated convolutions, group convolutions and deformable convolutions. We choose NVIDIA TensorRT as our baseline. The result of MXNet 1.4 + cuDNN 7.3 in float32 mode is reported to show the speed up of quantization. The experiments are conducted on NVIDIA GTX 1080. We report the inference time per image when running in batch size = 1 and 16.
As shown in the Figure 1, TVM achieves up to 8x speedup using quantization. In standard CNN models such as VGG and ResNet, TVM achieves parity with the state-of-the-art results from TensorRT.
When benchmarking emerging models, TVM achieves impressive results. We obtain significant performance gains on ResNeXt and DCN-ResNet-101. Results of DCN-ResNet-101 of TensorRT are not available because there is no official implementation of the deformable convolution. We show that automatic optimization in TVM makes it easy and flexible to support and optimize emerging workloads.
Show Me the Code
Bio & Acknowledgement
Wuwei Lin is an undergraduate student at SJTU. He is currently an intern at TuSimple. The author has many thanks to Tianqi Chen and Eddie Yan for their reviews.

